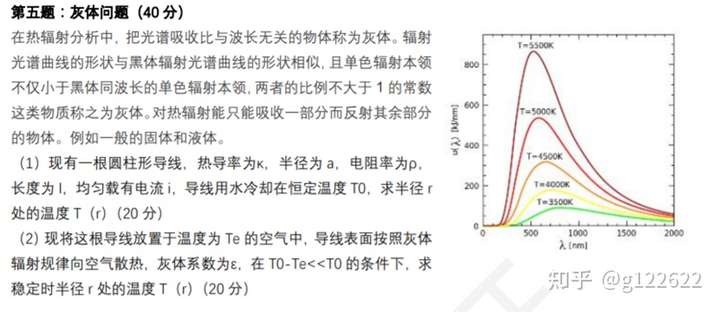
变分法练习题：求解旋转状态的绳子方程

最近看了一点某教授的变分课程（他写的教材应该是相对来说浅显易懂一些的了），想通过一些例题来巩固一下。

在菜市场里，我们可以看到这样的用来驱赶苍蝇的装置：

                ^图片，侵删^

在不考虑空气阻力的情况下，我想利用最小势能原理，求出下面吊着的这根绳子的函数表达式。

建立坐标系如下：

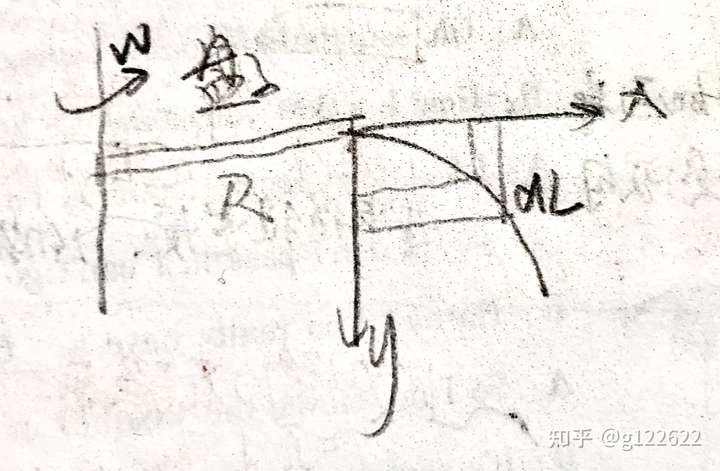
设绳子总长 ，圆盘半径 ，重力加速度 ，绳子线密度 。认为绳子上所有质元都处在同一平面。

设绳子形状对应函数 ，则单位长度

约束条件积分可得到

离心势能和重力势能共同构成质量元的势能，先来推导离心势能：

积分得到

重力势能表为

又有

2、3、4、5联立得

为了求势能最小值，利用Lagrange乘子法（这里我取了 为Lagrange乘子），此时Lagrangian为

代入Euler-Lagrange方程

还有边界条件

整理并部分展开，得到最终的表达式

---

另外，我问问怎么用matlab得到数值解？似乎很难整理出规范形式，带不进ode求解器。